一笔画的背后

今天排队论的老师讲起了图论hhh

让我想起了小时候看的有关一笔画的东西，能不能一笔画成的规律倒是知道，但竟一直没想过如何证明证明。

今天正好借着图论开课的机会重新想一想，然后就翻到了欧拉的证明，大道至简，清晰的思维值得记录。

开端

一笔画问题（Eulerian graph）是图论中一个著名的问题。一笔画问题起源于柯尼斯堡七桥问题。数学家欧拉在他1736年发表的论文《柯尼斯堡的七桥》中不仅解决了七桥问题，也提出了一笔画定理，解决了一笔画问题。

欧拉的研究是图论的开端。

莱布尼茨在1670年写给惠更斯的一封信中写道：

我不满足于代数，因为它既不能给出最短的证明，也不能给出最漂亮的几何结构。因此，考虑到这一点，我认为我们还需要另一种分析，几何的或线性的，直接处理位置，就像代数处理数值那样。

莱布尼茨的研究如今被称为 拓扑学，但作为一个数学领域在当时发展缓慢。正如高斯在1833年指出的

莱布尼茨开创了位置几何学，但当时只有欧拉和范德蒙（对，就是范德蒙行列式那位）两位几何学家对其略知一二。一个半世纪后，我们才懂得并掌握了这一几何学。

就是在高斯口中对几何学 略知一二 的欧拉的一篇论文，被誉为是西方现代图论的起点。

在数学界，18世纪被誉为是欧拉的时代。令人惊讶的是，欧拉的近900本书、论文和其他作品中，有近一半是在1771年几乎完全失明后写的。（天才况且如此……

在1736年的 Commentarii Academiae Scientiarum Imperialis Petropolitanae 上，欧拉对现在著名的柯尼斯堡桥问题进行了数学描述：有没有可能计划在柯尼斯堡镇漫步一次，但是这座镇上的七座桥每座桥只能穿过一次？

The problem, which I am told is widely known, is as follows: in K¨onigsberg in Prussia, there is an island A, called the Kneiphof ; the river which surrounds it is divided into two branches, as can be seen in Fig. [1.2], and these branches are crossed by seven bridges, a, b , c , d , e , f and g. Concerning these bridges, it was asked whether anyone could arrange a route in such a way that he would cross each bridge once and only once. I was told that some people asserted that this was impossible, while others were in doubt: but nobody would actually assert that it could be done. From this, I have formulated the general problem: whatever be the arrangement and division of the river into branches, and however many bridges there be, can one find out whether or not it is possible to cross each bridge exactly once?

像其他早期的图论工作一样，柯尼斯堡七桥问题看起来只不过是一个有趣的谜题。然而，从这种看似琐碎的起源，图论发展成为一种强大而深刻的数学理论，如今在物理、生物和社会科学中有着广泛的应用。

证明它！

简化

在开始证明之前，值得注意的是欧拉将城市复杂的画卷（见封图）抽象成了简单的草图，在现代图论中，我们进行了进一步的简化（仅保留点和连接点的线）。

方法

当然有一种大力出奇迹的方法可以证明这个问题，就是列出所有可能的情况，找不到符合题设的就OK了。但是这种方法有几点弊端：

• 不适用于更复杂的情况（兄弟，真的遍历不完的
• 不能抽象为理论！！（这很重要，琐碎变为伟大的关键
• 会浪费注意力在那些根本不可能成为答案的路径上

欧拉的整个方法依赖于一种特别方便的方式，用这种方式可以表示桥梁之间的关系。

问题表示方法

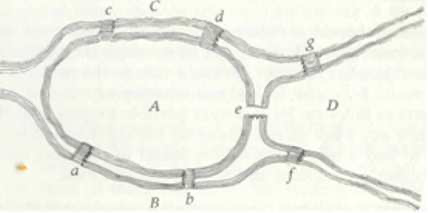
我们使用大写字母A、B、C、D表示河流分隔的每个陆地区域（见上图）。如果一个旅行者通过a桥或b桥从A到B，将其写为AB

AB中第一个字母指的是旅行者离开的区域，第二个字母指的是他过桥后到达的区域。

因此，如果旅客离开B，穿过f桥进入D，则该路径用BD表示，两个路径AB和BD的组合用三个字母ABD表示，其中中间字母B表示第一条路径结束的区域和第二条路径开始的区域。如果旅行者又穿过桥g从D到C，我将用四个字母ABDC来表示这三个连续的路径

这四个字母ABDC意味着旅行者从A开始，穿过B，再到D，最后到达C。

由于每个陆地区域都被一条河的支流隔开，若要走过A、B、C、D 四个地方，旅行者必须穿过三座桥。类似地，四座桥的连续跨越将由五个字母表示。所以一般来说，无论旅行者跨越多少座桥，他的旅程都可以由一个比桥的数量大一个的字母来表示。因此，跨越七座桥需要八个字母来代表它。

欧拉的这种表示方法使得图表本身对于解决问题变得不再必要，在现代图论中，我们用集合$V = {v_0, v_1, \ldots , v_n}$ 和集合 $E = {e_0, e_1, \ldots , e_m}$ 来表示，其中集合$V$ 代表顶点的集合， $E$ 代表连接顶点的边的集合。

如果有一条回路可以遍历所有的顶点而每一条边只走过一次，那这样的路就被称作欧拉路径（包含所有顶点的迹），也是本题设想要寻找的路径。

另有更严格的条件：欧拉回路（包含所有顶点的迹且首位相接）

存在吗？

因此，问题归结为找到由四个字母A、B、C、D组成的八个字母序列，其中A、B、C、D又重复。在寻找这样一个序列之前，先弄清楚是否有可能以这种方式排列字母（即找到题设路径），因为如果可以证明没有这样的排列存在，那么任何查找排列的工作都是毫无意义的。

为了尝试这样的规则，我考虑了单个区域A，有a、b、c、d 四座桥与A关连。让我们先来看看通向A的单个桥：如果一个旅行者穿过这座桥，他必须在穿越前或者在穿越后到达A，因此在任何一种情况下，字母a都会在上述表示中出现一次。如果有三座桥（比如a、b和c）通向A，如果旅行者穿过这三座桥，那么在他的旅程中，无论他是否从a开始他的旅程，字母a都将出现两次。类似地，如果五座桥通向A，那么在通过所有桥的表示中，字母A会出现三次。

因此，在柯尼斯堡七桥的问题的路线表示中，因为五座桥（a、b、c、d、e）通向A区，所以字母A必须出现三次。接下来，由于三座桥通向b，字母b必须出现两次；类似地，D必须出现两次，C也一样。因此，在一系列八个字母中，代表通过七座桥的路径，字母A必须出现三次，字母B、C和D各出现两次——但这不能在八个字母的序列中出现（$3+2+2+2>8$）。因此，这样的旅程不能跨越柯尼斯堡的七座桥。

更进一步，只要通往每个区域的桥梁数量是奇数，无论桥梁如何布置，都可以判断不可能一次旅行穿越每座桥梁而不重复。因为要满足条件的话所有字母必须出现的次数之和比桥的数量多一个，然而，像我们的例子中所发生的那样，事实上需要字母出现的数量大于桥梁的数量加一，那么这样的旅程永远无法完成。

怎样才会存在？

如果通向 A 的桥的数目是偶数，那么就必须考虑是否在 A 地出发

比如有两座桥 a、b 连接 A、B，那么在 A 出发的路径可以是 A B A ，否则是 B A B

如果有四座桥通向A，如果旅行者从A出发，那么在整个旅程中，如果他要穿过每座桥一次，字母A必须出现三次；如果他在另一个区域开始行走，那么字母A将出现两次。

如果有六座桥通向A，如果旅程从A开始，那么字母A将出现四次；如果旅行者没有从A开始，那么字母A只出现三次。

所以，一般来说，如果桥的数量是偶数，那么如果行程不是从A开始，A的出现次数将是这个数字的一半，如果行程从A开始，A的出现次数将比桥的一半多一个。

由于在任何旅程中，一个人只能从一个区域出发。这样就可以根据通往每个区域的桥梁数量，确定表示该区域的字母出现的数量。如果桥梁数量为奇数，为桥梁数量的一半加一；如果桥梁数量为偶数，则为其一半。最后，如果所有事件的总数等于桥的数量加上一，那么满足要求的行程将是可能的，并且必须从一个有奇数座桥通往它的区域开始。当然，如果得到的字母总数比桥梁数加一小一，那么旅程可以从一个桥梁数为偶数的区域开始，这样字母数将因此增加一。

请注意，欧拉对“表示该区域的字母出现次数”的定义取决于通向每个区域（顶点）的桥（边）的数量是偶数还是奇数。在当代图论术语中，入射到顶点$V$上的边数被称为顶点$v$的“度”。

因此，无论给出了什么样的桥梁布置，欧拉给出的以下方法将确定是否可以穿过每座桥梁：

• 首先用字母 A、B、C 等表示被水隔开的各个区域。

• 然后，取桥的总数加上一，把结果写在下面的工作上面。

• 第三，把字母A、B、C等写在一列中，并在每一个旁边写下通向它的桥梁的数量。

• 第四，用星号表示那些有偶数桥的字母。

• 第五，在每一个偶数旁边写下一半的数字，在每一个奇数旁边写下一半的数字加一。

• 第六，把这些数字加起来，如果这个总和小于或等于上面写的数字，也就是桥的数量加上一，就得出结论，满足要求的旅程是可能的。

  必须记住，如果总和比上面写的数字小一，那么旅程必须从标有星号的区域之一开始，如果总和相等，则必须从未标有星号的区域开始。

  柯尼斯堡镇七桥问题的求解：

  七座桥，$7+1=8$

  地区	相邻桥数	通过地区次数
  A	5	3
  B	3	2
  C	3	3
  D	3	2

  显然 $3+2+2+2>8$ 不满足题设

再举一个例子，假设有如下图的排布

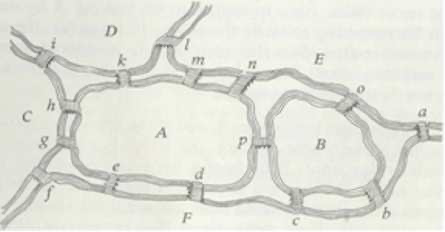
		16
A*	8	4
B*	4	2
C*	4	2
D*	3	2
E	5	3
F*	6	3
		16

按照上述规则，我们可以找到如下路径：

​ EaFbBcFdAeFfCgAhCiDkAmEnApBoEiD

这就是本题中的“欧拉路径”

更进一步

尽管上述方法已经可以在复杂的情况下找到欧拉路径（如果存在的话），但欧拉并没有止步于此，他找到了一种更抽象更简洁的方法来表达这一思想。

首先，观察到字母A、B、C等旁边写的桥的数量加起来是桥总数的两倍。原因是，在计算中，每一座通往某一特定区域的桥梁都会被计算两次，每一座桥梁连接的两个区域各计算一次。

因此，通往每个区域的桥梁总数必须为偶数（其一半等于桥梁数量）。进一步，字母A、B、C等的一些桥的数量中只有一个是奇数，或者三个是奇数，或者五个，等等，这是不可能的。因此，如果字母A、B、C等的一些桥的数量是奇数，那么这些区域的数量一定是偶数。

在七桥问题中，字母A、B、C和D都有奇数个桥相邻，在最后一个例子中，只有两个数字是奇数，即D和E。

上述结果也被称为“握手定理”，源于计算社交聚会期间发生的握手次数的等效问题。在社交聚会上，每个在场的人与其他在场的人握手一次。握手定理的现代表述是：“有限图中所有顶点的度之和等于图中边数的两倍。” 或 “每个有限图包含偶数个奇数度的顶点。”

由于字母 A、B、C 等所相邻的桥数的总和等于桥数的两倍。很明显，如果该总和增加2，然后再除以2，将得到我们所想要的数字（桥数加一）。因此，如果字母 A、B、C 等的所有数字（第二列）都是偶数，并且取其中的一半来获得第三列中的数字，那么这些数字的总和将比上面写的数字（桥数加一）少一个，而我们开始行走的地方需要加一，则无论是什么地方开始旅程，都可以找到符合要求的路径。在七桥问题中，如果旅行者两次穿过每座桥，就会发生这种情况（每座桥都可以被视为不同的两座）。

此外，如果字母 A、B、C 等所相邻的桥数中只有两个是奇数，其余的是偶数，那么，如果旅程从一个有奇数座桥梁通往的区域开始，那么得到符合条件的路径是可能的。因为，如果偶数减半，奇数增加一，它们的一半之和将比桥的数量大一，因此等于上面写的数字。从这可以进一步看出，如果有四，六，八……个奇数出现在第二列，那么第三列中的数字之和将比桥数大2，3，4……甚至更多。那么找到符合题设的路径将是不可能的。

至此，得到了为人们所熟知的结论，即：

无论桥如何排列，如果有两个以上的地区有奇数座桥梁通往，那么找到符合要求的路径是不可能的。
如果恰好有两个区域的桥梁数量是奇数，那么如果从这两个区域中的任何一个开始，找到符合要求的路径都是可能的。
如果没有奇数座桥梁通往的区域，那么可以从任何区域开始完成所需的旅程。

找到路径！

如果知道了在合适条件下必然存在符合题设路径，如何找到呢？ 关于这个问题，欧拉给出了答案（给了，但是又没给hhh）

欧拉原话：

I do not therefore think it worthwhile to give any further details concerning the finding of the routes.

理由是对于一个区域，我们可以成对的忽视桥梁，这样结构就被大大简化，所以便可以轻而易举的找到路径。

现代表述

要得到欧拉主要结果的完整现代陈述，我们需要几个定义

连通：

对于图 G 的两个顶点 u 和 v ，如果在中存在一条路，记为 (u,v) 路，则称 u 和 v 是连通的。如果图 G 不连通，则它每一个分支是连通的

根据这一定义，Euler论文的主要结果如下：

Theorem：有限图G包含Euler回路当且仅当G是连通的且不包含奇数度顶点。

Corollary：有限图G包含Euler路径当且仅当G是连通的且至多包含两个奇数度顶点。

当然，欧拉的证明与现代证明有所不同，但欧拉的这项工作为几何学特别是图论翻开了新的一页。

就这样，是否可以不重复的走遍七座桥 这样一个看似“没啥用”的问题，经过百年的发展，如今成为了可以许多学科问题的便利工具。

所以，多做点“没用的事”，挺好。